아래 사진은 2019년 1월 5일, 14일에 찍은 사진들을 담은 폴더를 캡쳐한 것이다. 여기 보면 유형에 JPG 파일이라고 적혀있는 것을 확인할 수 있다. JPEG 이미지 파일 형식으로 이미지가 저장 및 표현되어 있다는 뜻이다.
디지털 카메라, 스마트폰으로 찍은 사진은 대부분 디폴트 형식인 JPEG 형식으로 저장된다. 디폴트 형식이 JPEG이라는 것은 그만큼 JPEG으로 이미지를 저장하고 표현하는 것이 일반적이란 뜻이다. 오늘은 우리에게 친숙하고도 친숙한 JPEG이 도대체 무엇인지, 그 기반에 있는 기술에 대해서 알아보도록 하겠다.
JPEG에 대해 설명하기 전에 잠시 이미지 파일 형식이 무엇인지 살펴보고 가겠다. 왜냐하면 JPEG은 이미지 파일 형식의 한 종류이기 때문이다.
이미지 파일 형식이란?
이미지 파일 형식(image file format)은 이미지 데이터를 저장하고 표현하기 위한 파일 형식을 의미한다[1]. 이미지 파일 형식은 크게 래스터(raster) 방식과 벡터(vector) 방식으로 나눌 수 있다. 래스터 방식은 이미지를 색상 정보가 담긴 픽셀들로 표현하는 방식이고, 벡터 방식은 수학식으로 이뤄진 점, 직선, 곡선, 다각형 등으로 이미지를 표현하는 방식이다.
래스터 이미지는 픽셀의 수가 많을수록 화면의 질이 향상된다. 하지만 그만큼 파일 용량은 커진다. 또한 화질의 손실 없이 이미지의 사이즈를 확대시키거나 축소시키는 것이 불가능하다.
벡터 이미지는 아무리 이미지를 확대시켜도 선명하게 보인다. 확대 및 축소에 자유롭다는 뜻이다. 하지만 색상의 자연스러운 변화나 세밀한 표현이 어렵고, 과도하게 복잡한 계산이 필요한 이미지의 경우 컴퓨터에 큰 부담을 준다. 수행해야할 계산량이 많기 때문이다.
JPEG, GIF, PNG, TIFF, BMP, Raw 등이 래스터 방식을 이용한 이미지 파일 형식들이고, AI, SVG, VML, CGM, 거버 포맷 등은 벡터 방식을 이용한 것들이다. PDF와 EPS는 두 방식을 복합적으로 사용한 이미지 파일 형식들이다.
오늘은 이미지 파일 형식 중에서 래스터 방식에 속하는 JPEG에 대해서 정리하려고 한다. JPEG은 아마도 우리가 가장 많이 접하는 이미지 파일 형식일 것이다.
JPEG 이해하기
JPEG(Joint Photographic Experts Group)은 손실 압축 기술을 사용하는 이미지 파일 형식이다. 손실 압축이란 원본 파일의 용량을 줄이기 위해 고의적으로 이미지를 손실시키는 것이다. 단, 사람의 눈에 크게 거슬리지 않는 부분들을 손실시킨다. 사람의 눈은 이미지의 전체적인 구조가 손실되는 것에는 민감하지만, 디테일한 부분이 바뀌는 것에는 비교적 둔감하다. 이미지의 전체적인 구조는 저주파 성분과 관련되어 있고, 디테일한 부분은 고주파 성분과 관련되어 있다. 이러한 속성을 이용해서 고의적으로 고주파 성분의 일부를 제거하는 것이다. 이를 위해 이미지를 주파수 도메인으로 변환을 해준다. 이산코사인변환(DCT, discrete cosine transform)을 이용한다.
그러면 어떻게 이미지의 화질을 최대한 유지하면서 손실 압축시키는지 자세하게 한 단계 한 단계 살펴보자.
1) 이미지 색 공간 변환
RGB 색공간을 YCbCr 색공간으로 변환한다. Y성분은 픽셀의 밝기를 나타내고, Cb와 Cr은 색차성분을 나타낸다.
2) 다운샘플링(downsampling) 또는 서브샘플링(subsampling)
색공간을 변환해준 이유는 사람의 눈이 색상 성분보다는 밝기(휘도) 성분에 더 민감하기 때문에 밝기 정보보다 색상 정보를 더 많이 압축하기 위해서이다. 이를 위해 다운샘플링을 하는데, Y성분은 그대로 나두고 Cb와 Cr을 줄이는 방향으로 샘플링을 한다. 왜냐하면 색정보는 밝기정보보다 사람에게 덜 중요하니까.
서브샘플링 전략은 보통 J:a:b의 비율로 표현된다[7]. 여기서 J는 샘플링을 시행할 픽셀블럭의 너비를 의미한다. 보통 4로 설정된다. 픽셀블럭의 높이는 2로 정해져있다. 그리고 a는 J픽셀들의 첫번째 행에서 추출한 샘플들의 갯수를 의미한다. b는 J픽셀들의 두번째 행에서 추출된 샘플들의 갯수를 의미한다. 이게 무슨 말인지 이해가 안 될 것이다. 아래 그림을 참고하면서 좀 더 이야기해보자.
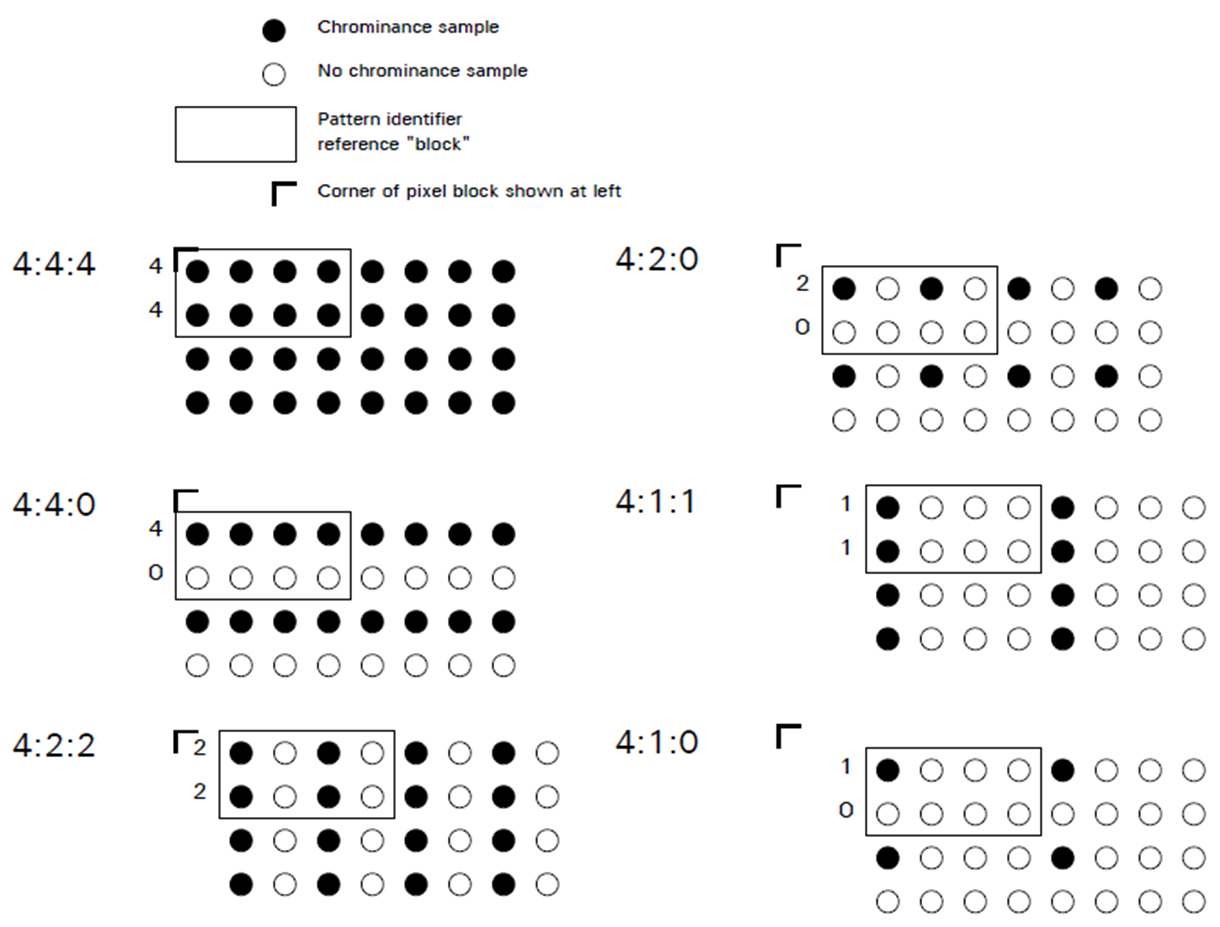
J값이 4인 경우, 즉 4:a:b일 때는 2 x 4 사이즈의 픽셀블럭에서 샘플들을 추출한다. 만약 J값이 8이라면 2 x 8 사이즈의 픽셀 블럭에서 샘플들을 추출할 것이다.
위 그림에서 4:4:4를 보면 첫번째 행과 두번째 행에서 모두 4개씩, 전부를 다 추출한다. 사실상 subsampling을 안하겠다는 뜻이다. 4:4:0을 보면 첫번째 행에서는 4개를, 두번째 행에서는 0개를 추출한다. 4:2:2는 첫번째 행과 두번째 행에서 각각 두개씩을 추출한다. 4:2:0은 첫번째 행에서 2개, 두번째 행에서 0개를 추출한다. 4:1:1, 4:1:0도 마찬가지다. 아래 그림을 보면 이제 확실히 이해할 수 있을 것이다.
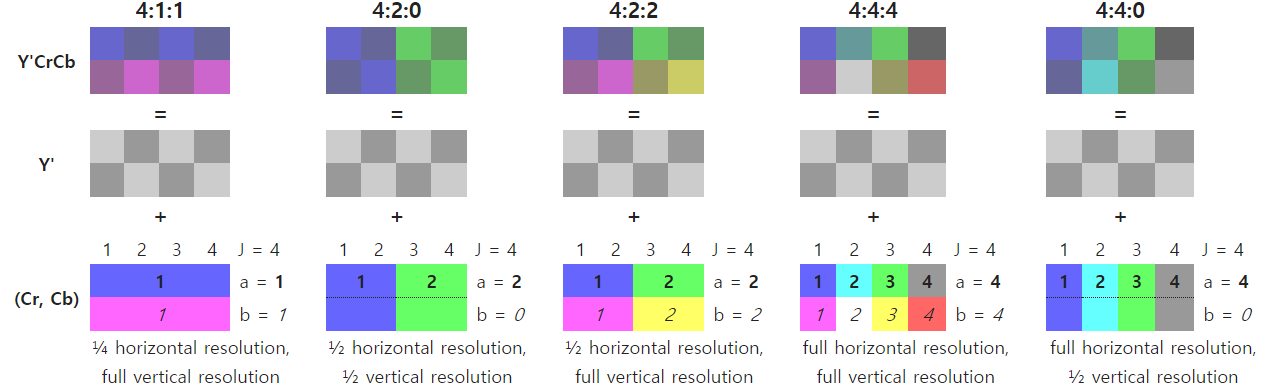
가장 아래 행을 보면 4:1:1에서는 1x4 픽셀의 색상값이 하나로 표현됨을 알 수 있고, 4:2:0에서는 2x2 픽셀의 색상값이 하나로 표현됨을 알 수 있다. 4:2:2에서는 1x2 픽셀의 색상값이 하나로 표현되고, 4:4:4에서는 1x1 픽셀의 색상값이 하나로 표현된다. 4:4:0에서는 2x1 픽셀의 색상값이 하나로 표현된다. 중요한 것은 Y성분은 서브샘플링하지 않고 그대로 놔둔다는 것이다.
JPEG에서는 주로 4:2:0 방식을 사용한다. 4:2:0 방식으로 Cb 성분과 Cr 성분을 서브샘플링해주면 8개 픽셀당 2개의 값을 추출하고 6개의 값을 버리게 되므로 그만큼 용량을 줄일 수 있다.
이어지는 압축 과정에서는 Y, Cb, Cr 채널들은 각각 분리되어 매우 유사한 방식으로 처리된다.
3) 이산코사인변환(DCT)
서브샘플링 후에 각 채널은 8x8 블락들로 분할된다. 4:2:0의 경우 Y채널은 8x8 블락들로, Cb, Cr채널들은 16x16 블락들로 분할된다고 보면 된다. 방식은 거의 동일하니 Y채널을 가지고 설명을 진행하겠다.
각 8x8 블락에 2D 이산코사인변환(DCT)을 적용한다. 그 결과 주파수 관점에서 이미지를 볼 수 있게 된다. JPEG 압축의 핵심을 기억해야한다. 고주파 성분을 줄임을 통해서 이미지의 용량을 줄이는 것!
예를 들어, 하나의 8x8 블락이 다음과 같다고 가정해보자.

각 8x8 블락에 DCT를 적용하기 전에 우선 [0, 255] 범위의 픽셀값들에 128을 빼줌으로 [-128, 127] 범위로 변경해준다. 그 다음에 DCT를 각 블락에 적용한다.

주파수 도메인에서 가장 왼쪽 위에 큰 절대값을 갖고 있는 계수(coefficient)를 DC 계수라고 부른다. 그리고 나머지 63개의 계수들은 AC 계수라고 부른다. 특히 DC 계수는 저주파 성분과 관련되어 있으며 해당 블락의 기본적인 명도를 결정하는 매우 중요한 정보를 담고 있다. 그리고 AC 계수들은 고주파 성분들과 연관되어 있다.
4) 양자화(quantization)
드디어 JPEG 압축에서 핵심적인 부분에 도달했다. 양자화는 고주파 성분을 제거하기 위한 방법이다. 주파수 영역의 각 계수에 대해 특정 상수(양자화 행렬)로 나눈 후 반올림한 값들을 취한다. 전형적인 양자화 행렬은 다음과 같다.

양자화행렬을 보면 DC계수 위치의 값은 비교적 작고 AC계수들 위치의 값들은 오른쪽 아래로 가면 갈수록 커지는 경향이 있음을 알 수 있다. 이 뜻은 DC계수는 작은 값으로 나눠준다는 뜻이고, AC계수들은 오른쪽 아래에 위치한 것일수록(주파수가 높은 것일수록) 더 큰 값으로 나눠준다는 뜻이다. 예를 들어, DC계수 -415.38은 16으로 나눈 후 반올림되기 때문에 -26의 값을 갖는다. 그 오른쪽에 있는 AC계수 -30.19는 11로 나눈 후 반올림되기 때문에 -3의 값을 갖는다. 이런 방식으로 양자화 행렬을 통해 양자화하면 다음과 같이 된다.
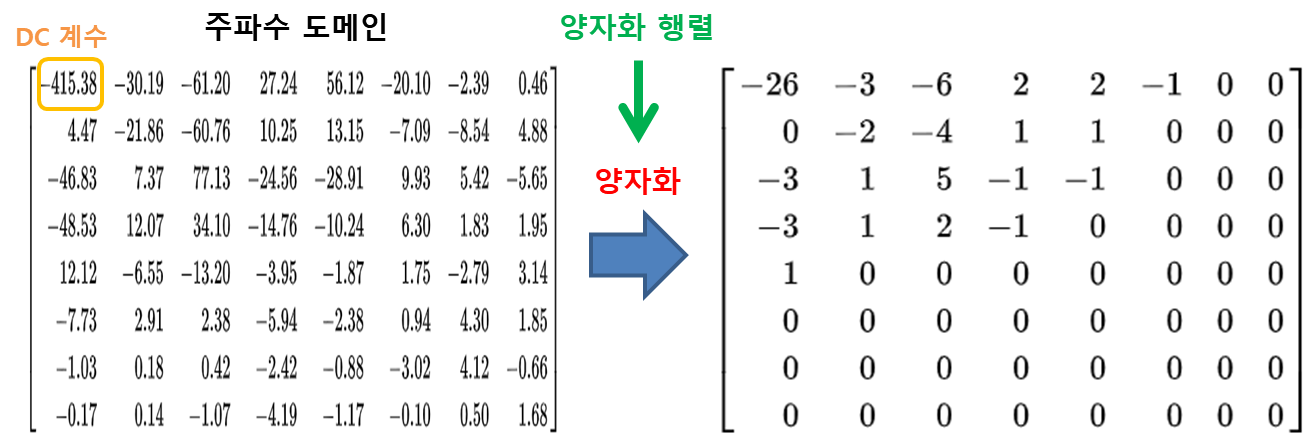
그 결과 많은 AC 계수들이 0이 되어 버린다. 이 말은 양자화를 통해 고주파 성분들을 손실시켰다는 뜻이다.
5) zigzag 스캐닝
2차원으로 배열되어 있는 양자화된 DCT 계수들을 1차원의 데이터로 만들어준다. 이때 쓰는 기법이 zigzag 스캐닝이다.
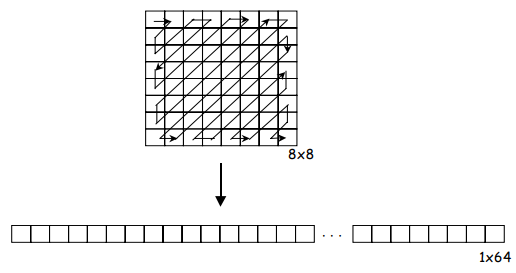
위 그림과 같이 지그재그 순서로 양자화된 DCT 계수들을 읽어서 쭉 나열하면 다음과 같은 1x64 사이즈의 벡터에 담을 수 있다.
[-26, -3, 0, -3, -2, -6, 2, -4, 1, -3, 1, 1, 5, 1, 2, -1, 1, -1, 2, 0, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
6) 양자화된 DC 계수 부호화
양자화된 DC계수와 AC계수는 각각 다른 방식으로 부호화한다. 먼저 DC계수 부호화에 대해 알아보자. DC계수는 해당 블럭의 기본적인 명도와 관련되어 있다고 위에서 언급했었다. 그러다보니 인접한 블럭들의 DC계수는 비슷한 값일 때가 많다. 따라서 이전 블럭의 DC 계수와 현재 블럭의 DC 계수의 차, 즉 변동값을 구한다. 작은 숫자일수록 더 적은 비트를 차지하기 때문이다. 이것을 DPCM(differential pulse code modulation)라고 부른다. 다음 그림을 보자.
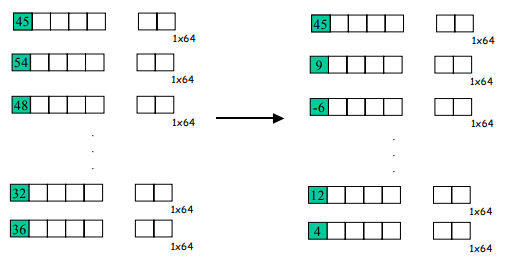
위 그림을 예로 삼으면 첫번째 블럭의 양자화된 계수가 45이고, 두번째 블럭의 양자화된 DC 계수가 54이므로, 54-45해서 9를 두번째 블럭의 DC 계수 자리에 넣는다. 마찬가지로 모든 블럭의 DC 계수를 다음과 같이 바로 전 블럭의 DC계수와의 차로 대체해준다. 그 다음에 이 차 값에 대한 허프만 부호를 허프만 코드표에서 참조하면 된다. 그러면 양자화된 DC값들에 대한 부호화는 마무리된다.
우리가 예를 든 블럭의 양자화된 DCT 계수에서 DC 계수값은 -26이다. 만약 바로 전 블럭의 DC 계수값이 -16이라면, DPCM에 의해 -26-(-16) = -10이 나올 것이다. 이것은 허프만 코드표를 참조하면 1010101로 부호화된다. 허프만 코드표를 참조하는 것은 여기서 굳이 다루지 않겠다. 참고자료 [9]에 잘 나와있으니 참고하시고 그래도 이해가 안되시면 질문해주시기 바랍니다.
7) 양자화된 AC 계수 부호화
나머지 63개의 양자화된 AC 계수들에 대해서는 런 렝스 부호화(run-length encoding)를 적용한다. 0이 아닌 양자화된 AC계수들을 다음과 같이 부호화하는 것이다. (앞에 0이 몇개 나오는지, 그리고 자신의 값은 얼마인지)
이해를 돕기 위해 간단한 예를 들어보겠다. 양자화된 DC 계수가 다음과 같다고 가정하자.
[9 5 0 0 4 0 0 0 3 0 0 0 0]
이것은 런 렝스 부호화에 의해 다음과 같이 부호화된다.
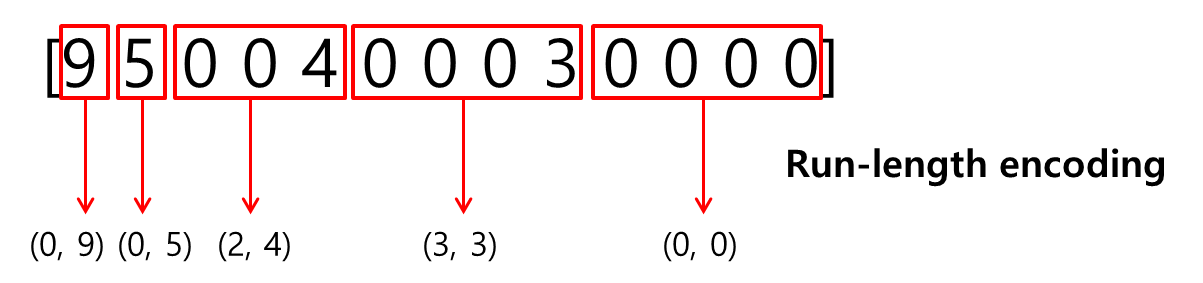
9 앞에는 0이 없으므로 (0, 9)로 부호화된다. 5앞에도 0이 없으므로 (0, 5)로 부호화된다. 4 앞에는 2개의 0이 있으므로 (2, 4)로 부호화된다. 3 앞에는 3개의 0이 있으므로 (3, 3)으로 부호화된다. 그 뒤로는 0밖에 없다. 이 나머지 0들은 (0, 0)으로 부호화한다. 이제 각각의 값에 대한 허프만 부호를 찾기 위해 허프만 코드표를 참조한다.
우리가 예로 들어온 양자화된 DCT계수에서 AC계수들만 적으면 다음과 같다. DC 계수 -26은 이미 1010101로 부호화되었다(전 블럭의 DC계수를 -16으로 가정하고 계산했었다).
[-3, 0, -3, -2, -6, 2, -4, 1, -3, 1, 1, 5, 1, 2, -1, 1, -1, 2, 0, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
런 렝스 부호화에 의해 AC 계수들은 먼저 다음과 같이 부호화된다.
(0, -3), (1, -3), (0, -2), ... , (5, -1), (0, -1), (0, 0)
그 다음에 허프만 부호화를 적용하면, 최종적으로 다음과 같이 부호화된다.
0100 11100100 0101 ... 11110100 000 1010
DC계수의 부호와 AC계수들의 부호들을 연결시키면 다음과 같아진다.
1010101 0100 11100100 0101 ... 11110100 000 1010
JPEG으로 이미지를 압축하면 이렇게 적은 수의 0과 1의 반복으로 이미지를 나타낼 수 있게 되는 것이다. 그만큼 많은 양의 용량을 아낄 수 있다. 하나의 8x8 8-bit 블럭을 표현하는데만 해도 최소 8x8x8=512의 비트가 필요한데, 다음과 같이 JPEG으로 압축하면 약 100비트 내외로 그 블럭을 표현할 수 있다. 약 400비트를 아끼게 되는 셈이다.
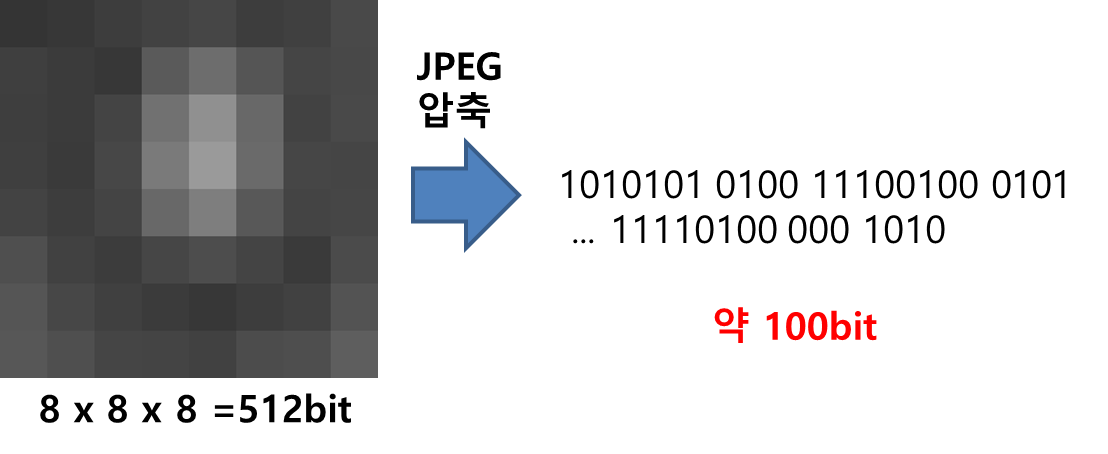
와우! JPEG을 만든 전문가 분들께 마음을 담아 존경심을 표합니다.
JPEG 압축과정을 요약하면 다음과 같다.
1) 이미지 색 공간 변환: RGB 색공간에서 YCbCr 색공간으로 전환한다.
2) 다운샘플링: 색과 관련된 채널들은 밝기 채널에 비해 덜 중요하므로 다운샘플링한다.
3) 이산코사인변환(DCT): 각 채널을 8x8 블럭으로 분할한 다음에 각 블럭마다 이산코사인변환을 시행한다.
4) 양자화: DCT 계수들을 양자화해서 높은 고주파 신호와 관련된 계수들은 대부분 0이 되게 한다.
5) zigzag 스캐닝: 2차원 배열에 담겨져 있는 양자화된 계수들을 지그재그 순서로 읽어 1차원 벡터가 되게 한다.
6) 양자화된 DC계수 부호화: DC계수들을 DPCM과 허프만 인코딩을 이용해 부호화한다.
7) 양자화된 AC계수 부호화: AC계수들을 런 렝스 부호화와 허프만 인코딩을 이용해 부호화한다.
이미지 파일 형식 중에 가장 대표적인 JPEG에 대해서 알아보았습니다. 누군가에게 도움이 되길 소망하며 글을 마칩니다.
이 글도 한번 읽어보세요 ☞
"JPEG2000 압축이 JPEG 압축보다 더 낫지만, 시장은 JPEG 압축을 선택했다"
최소식별차(just-noticeable-difference)와 영상압축
<참고자료>
[1] https://terms.naver.com/entry.nhn?docId=5682324&cid=43667&categoryId=43667, 네이버 지식백과 "이미지 파일 형식"
[2] https://ko.wikipedia.org/wiki/%EB%9E%98%EC%8A%A4%ED%84%B0_%EA%B7%B8%EB%9E%98%ED%94%BD%EC%8A%A4, 위키백과 "래스터 그래픽스"
[3] https://m.blog.naver.com/plipop/220673521161, 아임웹캠퍼스의 해준 "비트맵(래스터) 이미지와 벡터(Vector) 그래픽의 차이"
[4] https://en.wikipedia.org/wiki/JPEG, 위키백과(영어) "JPEG"
[5] https://ko.wikipedia.org/wiki/JPEG, 위키백과(한글) "JPEG"
[6] https://en.wikipedia.org/wiki/Chroma_subsampling, 위키백과(영어) "Chroma subsampling"
[7] http://dougkerr.net/Pumpkin/articles/Subsampling.pdf, Douglas A. Kerr "Chrominance Subsampling in Digital Images"
[8] http://www.cmlab.csie.ntu.edu.tw/cml/dsp/training/coding/jpeg/jpeg/encoder.htm, cmlab "JPEG encoding process"
[9] https://users.ece.utexas.edu/~ryerraballi/MSB/pdfs/M4L1.pdf, "Image Compression: JPEG" => 이 글도 매우 좋다.
'Research > 컴퓨터비전, 영상처리' 카테고리의 다른 글
| [IQA] 미리 훈련된 CNN으로 얻은 특성맵들의 품질로 이미지의 품질을 평가하는 모델, DeepSim (0) | 2019.07.10 |
|---|---|
| [Visual saliency] 중요 물체 검출(salient object detection, SOD)이란? (2) | 2019.07.06 |
| 경험 품질에 관한 레이블, MOS(mean opinion score)와 DMOS(differential opinion score) (0) | 2019.07.05 |
| semantic segmentation의 목적과 대표 알고리즘 FCN의 원리 (16) | 2019.05.31 |
| visual masking이란? (0) | 2019.05.07 |
| Bag of Words (BoW) 이해하기 (0) | 2019.04.17 |
| 이미지 라벨링 툴 labelImg 사용 중 에러 해법 (0) | 2019.04.12 |
| 물체 검출 알고리즘 성능 평가방법 AP(Average Precision)의 이해 (67) | 2019.04.09 |